前回に続き、単純なランバート+フォンシェーディングからステップアップして、PBR のレンダリング方法を勉強しています。直接光を対象とした計算については、所定の数式や各種テクスチャマップを使えば比較的スムーズに正しいとされる描画が実現できます。一方で、環境光を考慮し出すと一気に複雑になってくるように私は感じました。
環境光として環境マップを使用する
ここでは多くのものがそうであるように、環境光については環境マップとして保存された画像データを使います。イメージベースドライティング(Image Based Lighting:IBL) ですね。この環境マップとして使用するデータは、各画素が8bitでは足りないので、HDR (High Dynamic Range)で記録された画像形式を使います。各所で公開されているものの多くは、.hdr 形式か、.exr 形式かといったところですが、このようなものを使用します。
データの入手
私がよく使用するのは、以下のサイトです。HDRで記録された緯度経度のパノラマ画像となっています。
データの変換
DirectXを使用している場合、テクスチャの読み込みには DirectXTex を使うことも多いと思います。ただし DirectXTex は標準で EXR に対応していないので、テクスチャ形式を変更が必要です。 .EXR を読み込み、 .DDS や .HDR の形式に変換をするツールが必要です。このとき、SDRに変換せずに高輝度の情報をそのまま変換する必要があるので、私は NVIDIA の Texture Tools Exporter を使いました。
NVIDIA Texture Tools Expoter は、以下のページからダウンロードができます (要アカウント)。
なお、 .hdr から .dds の変換であれば、 DirectXTex シリーズの変換ツールである、texconv で変換も出来ます。
texconv.exe EveningEnvironmentHDRI003_2K-HDR.hdrIBLで描画するための事前処理
環境マップの準備ができたら、それを基にIBLで描画するための事前処理を実装します。計算式の導出や歴史的背景については、本記事では省略します。私も参考にした、以下の2つの情報を参照してもらうのがよいと思います。かなり分かりやすいと思うのでお勧めです。

さて、レンダリングの前に必要になるのは、環境マップから作成した以下のデータ (IBLテクスチャとLUT)です。これを生成する処理を Prefilter 処理と呼ぶこともあるようです。
- ディフューズ用 IBL テクスチャ
- スペキュラー用 IBL テクスチャ
- GGX用 BRDF テクスチャ (LUT)
いずれも生成のためにはレンダリング方程式をみながら、モンテカルロ積分を使い、重要度サンプリングによって基となる環境マップから生成するという手順となっています。基本的には、「Direct3D12ゲームグラフィックス実践ガイド」の書籍を追いかけてもらうのがよさそうなので、ここでは詳細はスキップします。
書籍にもあるようにパノラマ画像のままでは少々扱いにくかったため、キューブマップに変換してから処理をしていきます。

ディフューズ IBL テクスチャ
ディフューズ IBL テクスチャは、照度マップ (Irradiance map) とも呼ばれます。「Direct3D12グラフィックス実践ガイド」の方法に従って、ミップマップフィルタリングあり・なしで作成したものが以下となります。

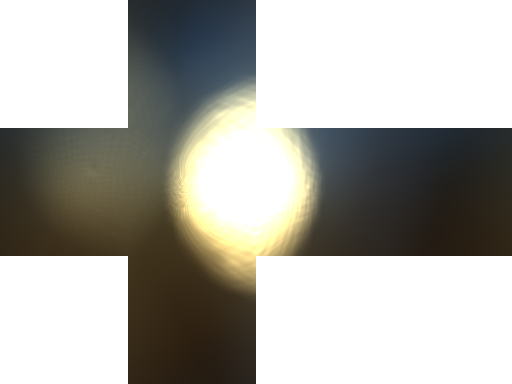
気になったので、もう少し調べてみました。LEARN OPENGL のサイトにも Diffuse irradiance の章(https://learnopengl.com/PBR/IBL/Diffuse-irradiance)があり、そこでは別の処理方法が記載されています。具体的には、インポータンスサンプリングで求めるのではなく、微少区間に区切って数値積分するタイプで求めます。使用している計算式を引用すると、
$$
L_o(p, \omega_o) = k_d \frac{c}{\pi}\int_{\Omega}L_i(p, \omega_i)n \cdot \omega_i d\omega_i
$$
これを半球状の球に適用し、式を変形すると、以下のようになります。
$$
L_o(p,\phi_o,\theta_o) = k_d \frac{c}{\pi}\int_{\phi=0}^{2\pi} \int_{\theta=0}^{\frac{1}{2}\pi} L_i(p, \phi_i, \theta_i) \cos(\theta) \sin(\theta) d\phi d\theta
$$
これを数値積分用に離散化した式を作ると、 \(\phi = [0, 2\pi], \theta = [0, \frac{\pi}{2}]\) の範囲になるので、
$$
\begin{align}
\Delta \phi &= \frac{2\pi}{N1} \\
\Delta \theta &= \frac{\pi}{2 N2}
\end{align}
$$
そのため、
$$
\begin{align}
d\omega &\approx \sin(\theta)d\theta d\phi \\
&= (\frac{2\pi}{N1}) \cdot (\frac{\pi}{2N2}) \cdot \sin(\theta)
\end{align}
$$
定数項を前に出して整理すると、
$$
\begin{align}
L_o(p,\phi_o,\theta_o) &= k_d \frac{c \pi}{n_1 n_2}\sum_{\phi=0}^{n_1} \sum_{\theta=0}^{n_2} L_i(p, \phi_i, \theta_i) \cos(\theta) \sin(\theta) d\phi d\theta
\end{align}
$$
こちらの実装では以下のような結果となりました。

その他、注意事項
「Direct3D12グラフィックス実践ガイド」の方法に従って、マップを作成した際に、以下のような気になる状態が起こります。精度のために、「Building an Orthonormal Bais, Revisited」の論文を参考にして、タンジェントスペースから変換をするところにおいて、発生してしまうようで、法線方向は一致だがタンジェントおよびバイノーマルが区切り線のところで反転するような生成になるように思われます。 なお、ミップマップフィルタリング有効で作成した場合には、このように目立つ結果にはなりませんでした。
スペキュラーIBL テクスチャ
スペキュラー IBL テクスチャ(放射輝度マップ) と、GGX BRDFのLUTを作るための重要な計算式は以下の通りです。ここに到達するまでには歴史や数式の変形がありますが、詳細については既に挙げた参考文献を参照してください。 (https://learnopengl.com/PBR/IBL/Specular-IBL の解説もよいです)
$$
\frac{1}{N}\sum_{k=1}^{N}\frac{L_i(l_k)f(l_k, v)\cos\theta_{l_k}}{p(l_k, v)} \approx
\Big( \frac{1}{N}\sum_{k=1}^{N}L_i(l_k)\Big) \Big(\frac{1}{N}\sum_{k=1}^{N}\frac{f(l_k, v)\cos \theta_{l_k}}{p(l_k, v)}\Big)
$$
この左辺から右辺へは近似です。近似によって、計算する対象を2つに分離するのが目的です (Split Sum Approximation という)。 近似した結果、左側は光源に関する情報、右側はBRDFの情報となっています。
放射輝度マップ (Specular LD)
「Direct3D12グラフィックス実践ガイド」の方法に従って、このマップも作成できます。キューブマップのサイズを合わせて、アニメーションにしてみたものが次の通りです。ラフネスに応じて参照するミップマップが変わることを考えると、よい感じの生成になっているのではないでしょうか。(ここでは 4×4 までで作成)

BRDF LUT (GGX)
書籍にあるコードで BRDF LUT を作成すると、以下のようなテクスチャとなります。分かりづらいかもしれませんが、縁が少々異常な状態になっています。これは計算の過程で NaN が入っているため発生するようです。
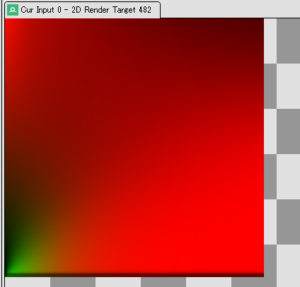
なお、コンピュートシェーダーで実装しても同様なので、ゼロ除算には注意しましょう。OpenGL で実装した場合 (https://learnopengl.com/PBR/IBL/Specular-IBL) では、この症状が出ず、なぜかを見ていたら、半テクセルのオフセットが掛かっていてゼロ割が回避されていたのでした。
glTF ビューワー方式の放射輝度マップ (Specular LD)
つぶつぶ感があったので、glTF Viewerを参照しながら、実装を少し変えて Specular LDを作成したのが以下のものです。

実装中に \(D_{GGX}\) 関数の実装が、少々気になる書き方をしていたので疑問に思いました。しかし、これについては式を変形した結果ということが分かりました。以下に式変形を記録しておきます。ここでは慣例に従い、 \(\alpha=roughness \times roughness \) です。
$$
\begin{align}
D_{GGX}(N,H,\alpha) &= \frac{\alpha^2}{\pi \cdot ((N \cdot H)^2 \cdot (\alpha^2-1)+1)^2} \\
&= \frac{1}{\pi} \Big( \frac{\alpha^2}{(1 – (N \cdot H)^2 + (N \cdot H \times \alpha)^2)^2} \Big) \\
&= \frac{1}{\pi} \Big( \frac{\alpha}{1 – (N \cdot H)^2 + a^2} \Big)^2
\end{align}
$$
途中で、\(N\cdot H \times\alpha = a \)と置換えると、このようになります。これでビューワー上でのシェーダーコードでの実装と一致します。
試しにレンダリング
それぞれのIBLをサンプリングして描画してみるとこのような感じです。それなりに合っているようにみえますね。


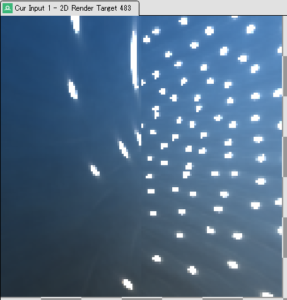
やはり気になるのは、ミップマップフィルタリング無しでDiffuse IBLを生成したものだと、以下のような結果になるということろで、何か課題が潜んでいるのかもしれません。

まとめ
お試しのレンダリングをさせてみて、 ミップマップフィルタリング無しのDiffuse IBLの結果をみたら、力(気力?) が尽きたので今回はここまでです。うまくいっている分の2つのIBLを使うと、そこそこ期待する間接光の描画ができるとは思われます。
その他、参考情報など
おまけ
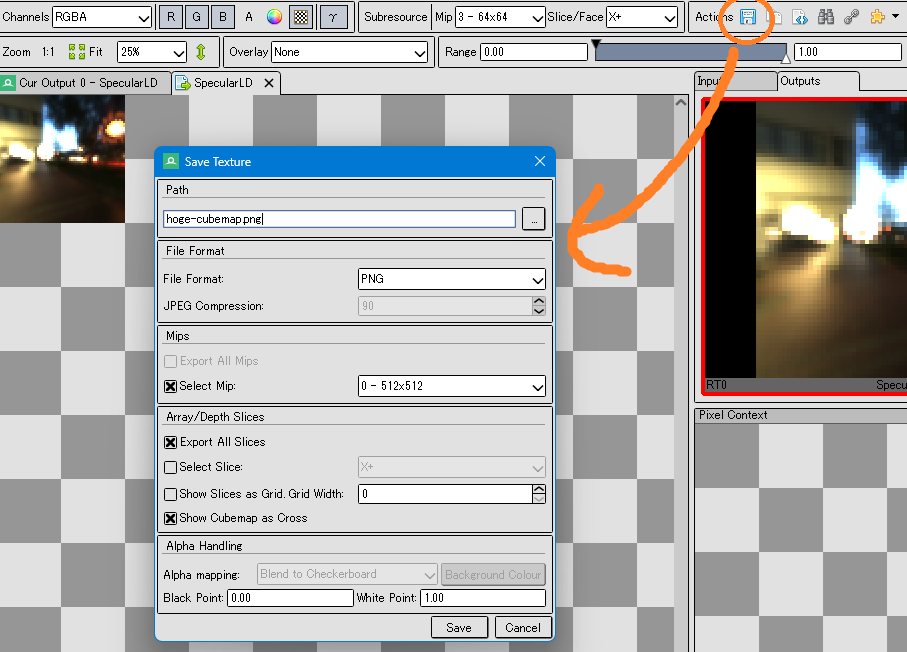
RenderDoc でキューブマップを開いているとき、保存ボタンからクロス表示された画像で保存が可能です。下記の画像に示すような設定で出力すると、キューブマップのクロス表示で保存できます。ここではブログ用にPNGを選択しましたが、DDSや、HDR, EXR 形式なども選べるようになっています。

コメント